经过学习，我们可以使用基本的机器学习模型解决了tabluar数据，可以理解为特征列互换训练模型，使用CNN卷积网络对图片类型的数据进行操作，生活中我们更加常见的还有序列模型“sequence data”，比如文本、视频、声音、股票的涨幅波动，它的数据之间具有较强的依赖性以及特定的顺序。下面我们主要针对文本序列展开探讨：

单词向量化表示

目前这里我们可能遇到的第一个问题是如何表示一个单词：

离散表示

独热编码表示（One-hot Encoding Representation）

比如我们想要表示“machine learning”这两个单词，经过分词我们知道它是由两个的单词组成的，假设我们拥有一个长度为5语料库：[I machine you learning he]，此时表示“machine”即为向量[0 1 0 0 0]，“learning”可表示为向量[0 0 0 1 0]，得到单词的向量化表示。

  • 优点：简单，便捷

  • 缺点：1. 此种向量化表示是基于独立性假设展开，但实际中应该考虑语料的顺序；2. 当语料词库比较大的时候，向量表示会十分稀疏，从而耗费大量的计算资源；3. 没有考虑词频表达影响。

词袋模型（Bag of Word）

参考https://en.wikipedia.org/wiki/Bag-of-words_model

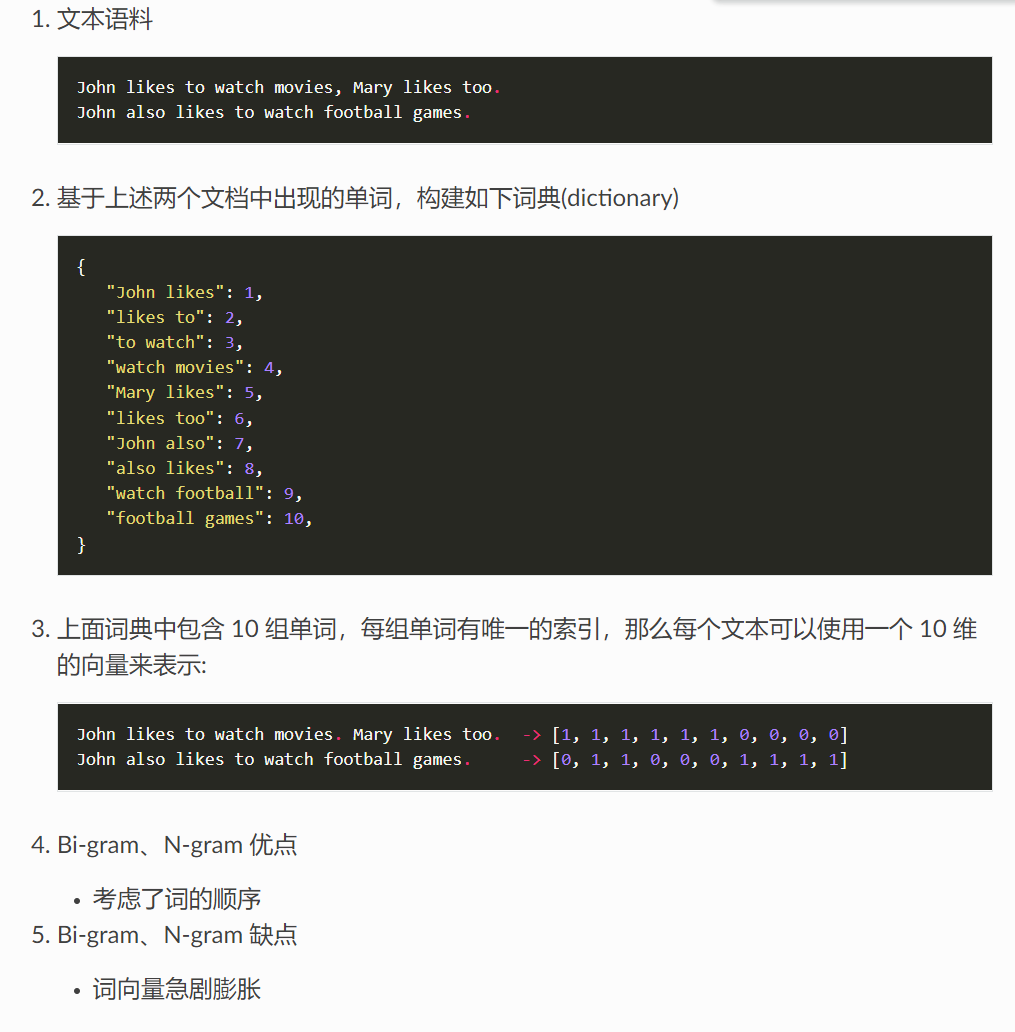
例如下面两条文本的表示：

s1 = "John","likes","to","watch","movies","Mary","likes","movies","too"

s2 = "Mary","also","likes","to","watch","football","games"

给予固定的序列，后面的数字表示其索引

{
   "John": 1,
   "likes": 2,
   "to": 3,
   "watch": 4,
   "movies": 5,
   "also": 6,
   "football": 7,
   "games": 8,
   "Mary": 9,
   "too": 10,
}

这样两条文本按照固定序列，数字表示词频，可分别表示为，：

BoW1 = {"John":1,"likes":2,"to":1,"watch":1,"movies":2,"Mary":1,"too":1};
BoW2 = {"Mary":1,"also":1,"likes":1,"to":1,"watch":1,"football":1,"games":1}
  • 优点：考虑了词频
  • 缺点：未考虑语序

N-gram

image-20221105155749068

TF-IDF

待添加

分布式表示

Word Embedding-word2vec

李宏毅无监督学习. https://www.youtube.com/watch?v=X7PH3NuYW0Q&ab_channel=Hung-yiLee

Word Embedding-GloVe

待添加

训练

1.word2vec 版本

语言模型

当我们可以对单个单词进行向量化表示之后，接下来应该考虑的是如何表示一段特定语序的文本，基于数理统计方法，给定文本序列$x_1,…,x_T$，语言模型的目标是估计联合概率$P(x_1,…,x_T)$：

语言模型常见应用：

  • 用作预训练模型（例如：BERT，GPT-2，3等）
  • 生成文本，给定文本前几个词，根据文本序列概率续写文本
  • 判断哪条序列更为常见，常用于机器翻译，选择更合适的翻译序列

词频统计（Word Frequency）

给定所有文本n，则序列长度为2的概率为，其余序列类似： $$ p\left(x, x^{\prime}\right)=p(x) p\left(x^{\prime} \mid x\right)=\frac{n(x)}{n} \frac{n\left(x, x^{\prime}\right)}{n(x)} $$ $n$表示总词汇，$n(x),n(x^{\prime})$是单个单词和连续单词次数

马尔可夫模型和N-grams（Markov modles ）

  • 基于词频统计的语言模型，因文本量不够大，可能$n\left(x_1, \ldots, x_T\right) \leq 1$
  • 二元和三元比较常用，代码中可提前存储所有组合可能性进行查询实现其功能，减少计算复杂度
  • 以下对用的语言二元模型

$$ p\left(x_1, x_2, x_3, x_4\right) =p\left(x_1\right) p\left(x_2 \mid x_1\right) p\left(x_3 \mid x_2\right) p\left(x_4 \mid x_3\right)\ =\frac{n\left(x_1\right)}{n} \frac{n\left(x_1, x_2\right)}{n\left(x_1\right)} \frac{n\left(x_2, x_3\right)}{n\left(x_2\right)} \frac{n\left(x_3, x_4\right)}{n\left(x_3\right)} $$

交叉熵（Perplexity）

Partitioning Sequences

循环神经网络（Recurrent Neural Network）

使用Markov模型可以简化语言模型，但是实际中，我们需要模型保留在$t-1$时刻的模型状态，因此可以简化语言为： $$ P\left(x_t \mid x_{t-1}, \ldots, x_1\right) \approx P\left(x_t \mid h_{t-1}\right) $$ 此处的$h_t$为隐藏状态，一般可写为： $$ h_t=f(x_t,h_{t-1}) $$

无隐藏状态的神经网络

此处考虑只有单隐藏层的MLP模型，给定的激活函数为$\phi$，给定minibatch为$\boldsymbol{X} \in \mathbb{R}^{n \times d}$拥有$n$个样本，及对应$d$个特征，此时隐藏层对应输出为$\boldsymbol{H} \in \mathbb{R}^{n \times h}$计算为，隐层包含的神经元的个数为$h$：

$$ \boldsymbol{H}=\phi(\boldsymbol{X}\boldsymbol{W}_{xh}+\boldsymbol{b}_h) $$

在上式中，权重$\boldsymbol{W}_{xh} \in \mathbb{R}^{d \times h}$，偏差$\boldsymbol{b}_h \in \mathbb{R}^{1 \times h}$，该模型仅有单个隐藏层，则对应的输出为：

$$ \boldsymbol{O}=\boldsymbol{H}\boldsymbol{W}_{hq}+\boldsymbol{b}_q $$

上式中，输出变量$\boldsymbol{O} \in \mathbb{R}^{n \times q}$，权重$\boldsymbol{W}_{hq} \in \mathbb{R}^{h \times q}$，偏差$\boldsymbol{b}_q \in \mathbb{R}^{1 \times q}$，如果是分类问题，我们可以对输出再添加Softmax函数进行概率估算。

有隐藏状态的神经网络

假设我们在$t$时刻小批量输入minibatch为$\boldsymbol{X} \in \boldsymbol{R}^{n \times d}$，对应的 $\boldsymbol{W}_t \in \mathbb{R}^{d \times h}$ ，偏置为$\boldsymbol{b}_t \in \mathbb{R}^{1 \times h}$，如果不考虑隐藏状态传递的信息，则对应的输出与MLP模型相同，当需要考虑前一个时刻的隐藏状态，为保证模型满足矩阵相乘条件，则$\boldsymbol{W}_t \in \mathbb{R}^{h \times h}$ ，因此对应的隐藏状态为（这里也可以添加偏置$\boldsymbol{b}$）：此处公两条LaTex公式显示有问题，暂用图片代替

$$ \boldsymbol{H}{t}=\phi(\boldsymbol{X}{t}\boldsymbol{W}{xh}+\boldsymbol{H}{t-1}\boldsymbol{W}_{hh}+\boldsymbol{b}_h) $$

MommyTalk1667782088297

同时$t$时刻对应的输出为：

$$ \boldsymbol{O}t=\boldsymbol{H}{t}\boldsymbol{W}_{hq}+\boldsymbol{b}_q $$

MommyTalk1667782179623

如果用于词性的判断或者分类、LSTM模型等，可以给输出再添加Softmax进行标签分类，这里引用其他图片说明：

../_images/rnn.svg
  • RNN相对于普通的全连接层，其实就是多了一步去计算$t-1$时刻的隐藏状态，因而可学习的参数更多
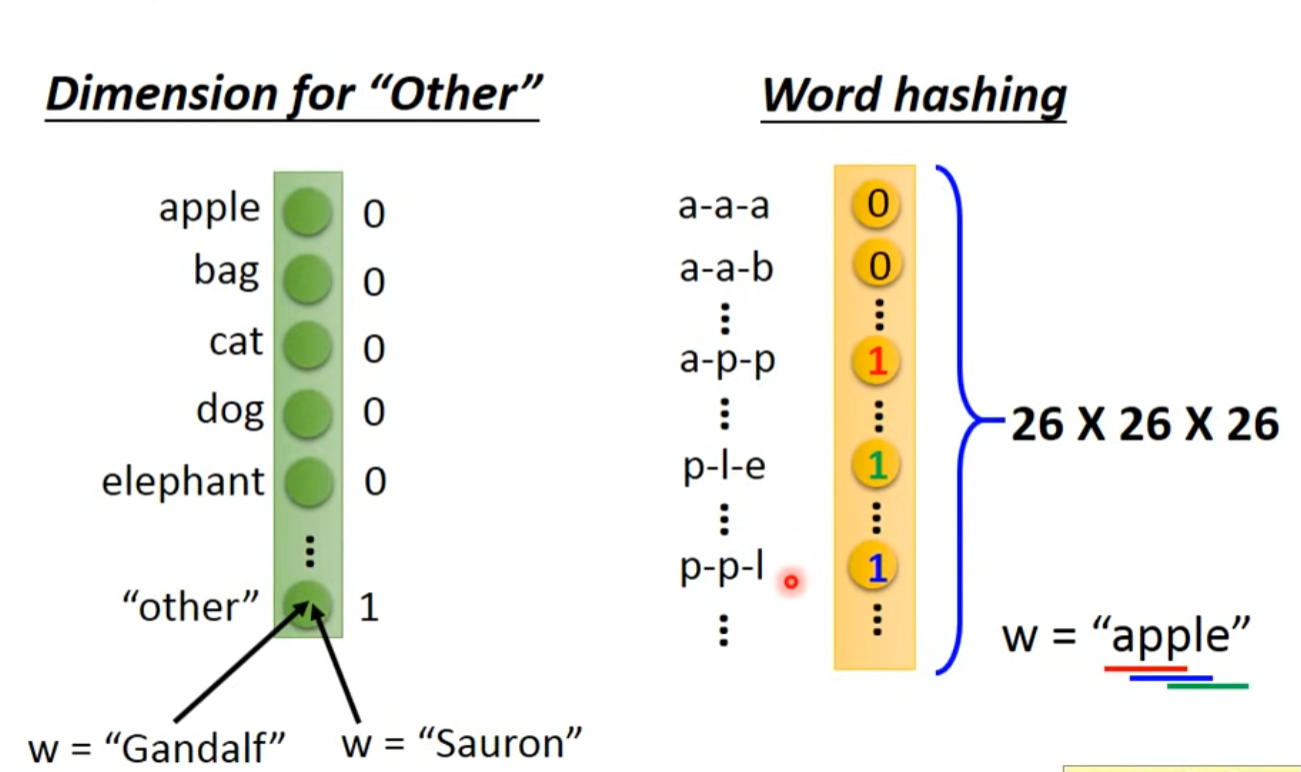
image-20221104170345716
  • 可以使用one-hot表示文本序列，一条文本语句就可以被表示为向量
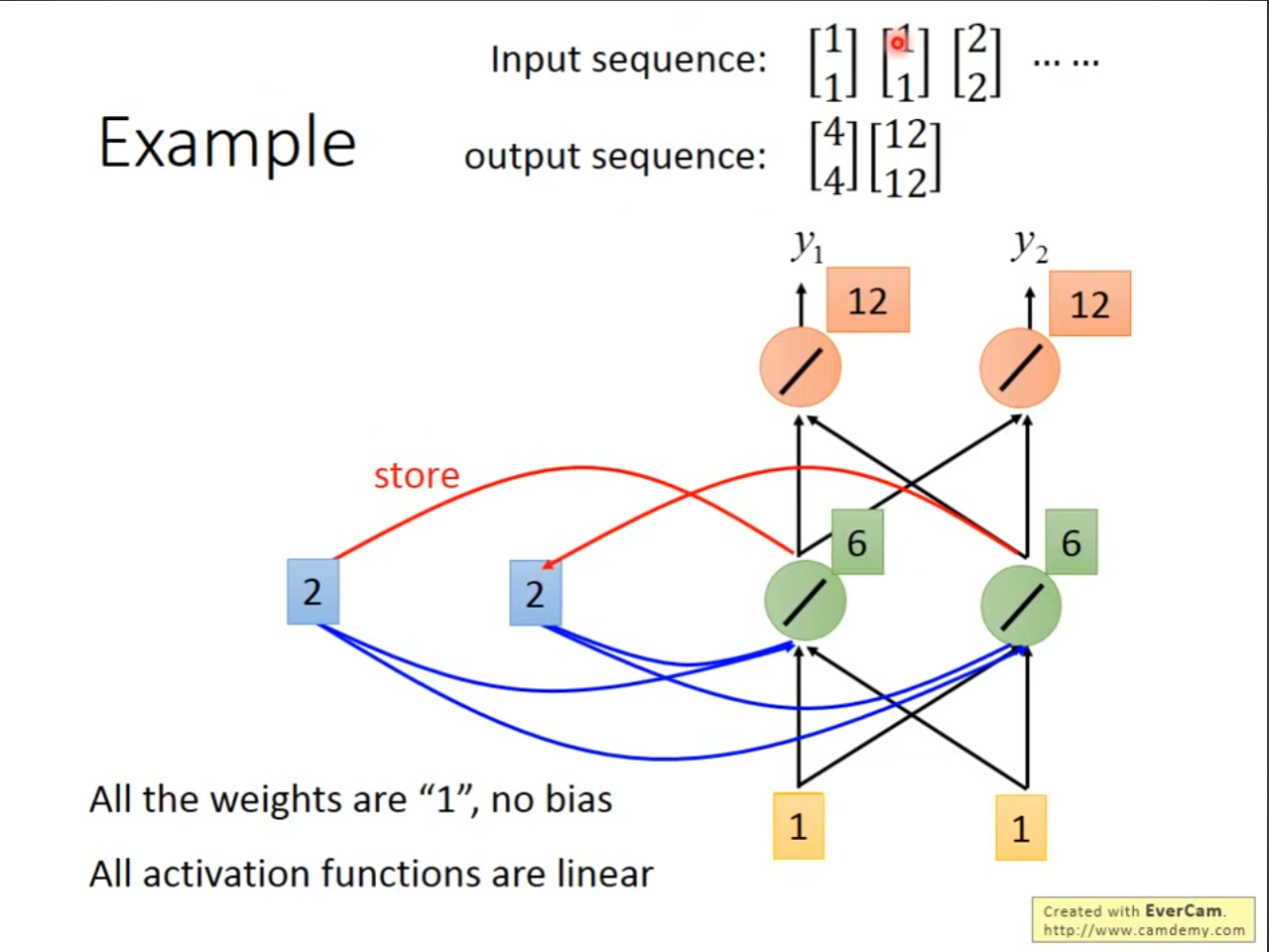
image-20221104171437780
  • 假设初始化隐藏状态w为1，为hidden layer
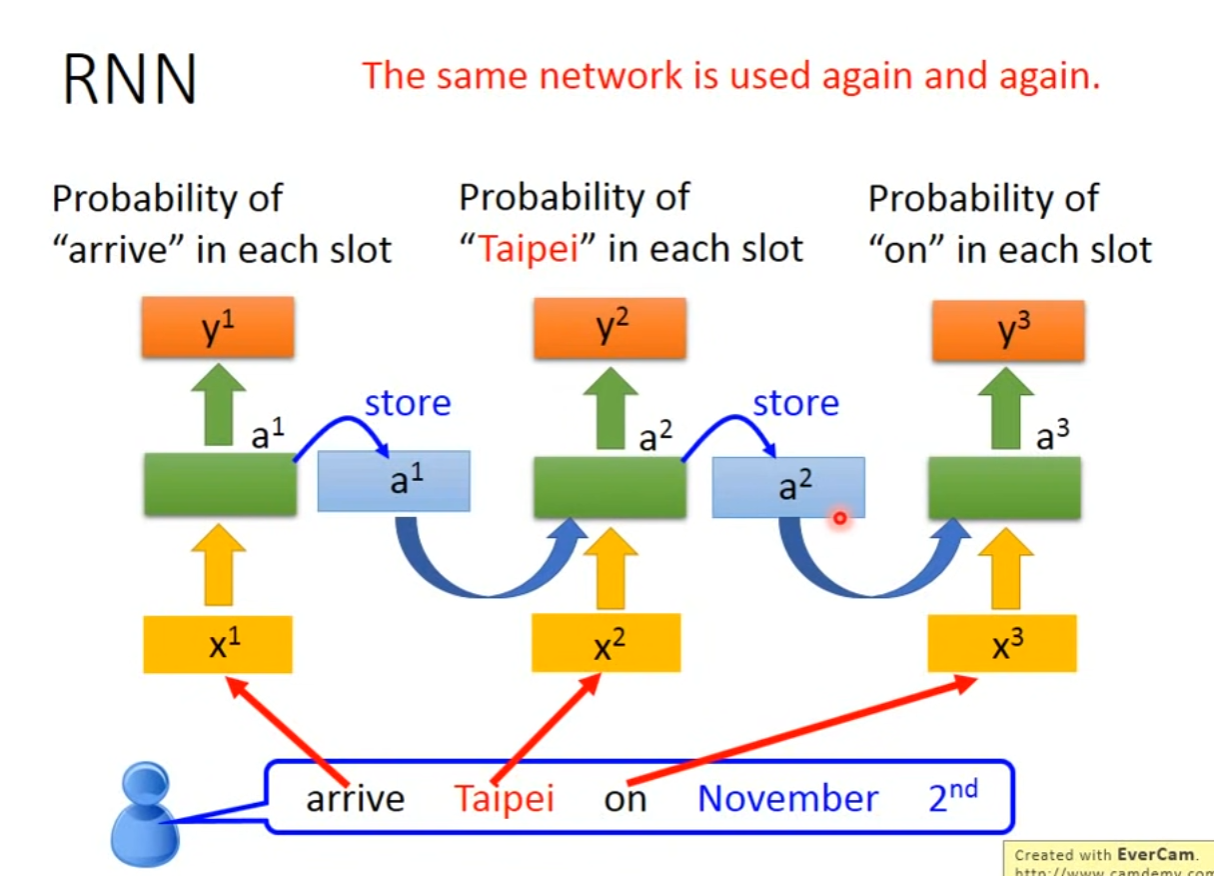
image-20221104171643247
  • 可以分辨一词多义
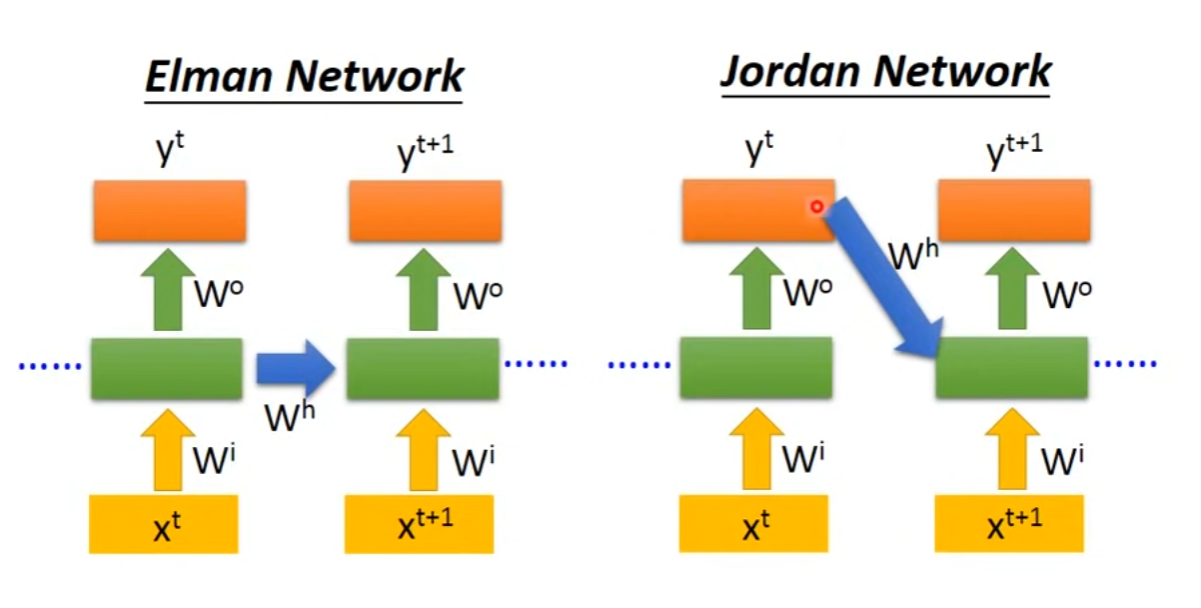
image-20221104171914006
  • 不同类型的RNN
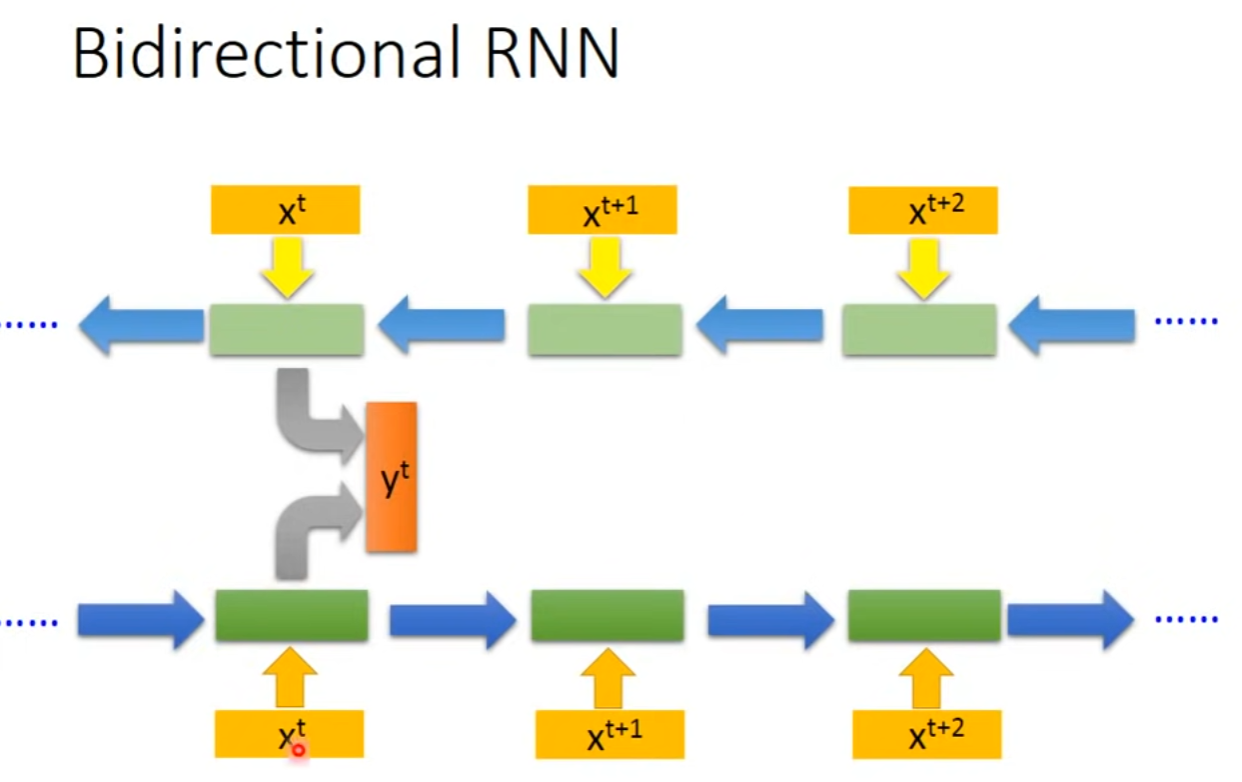
image-20221104172050764
  • 模型读取文本的范围更广

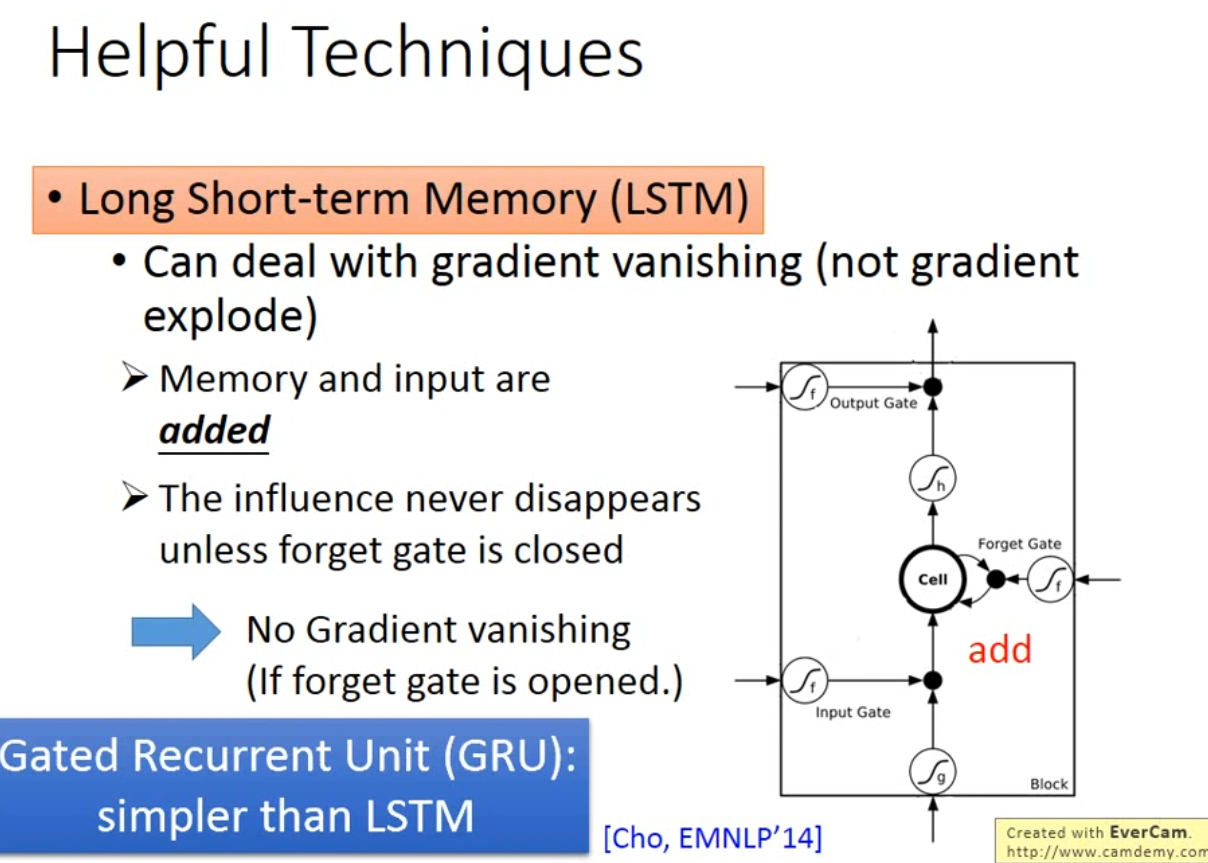
Long Short-Term Memory(LSTM)part1

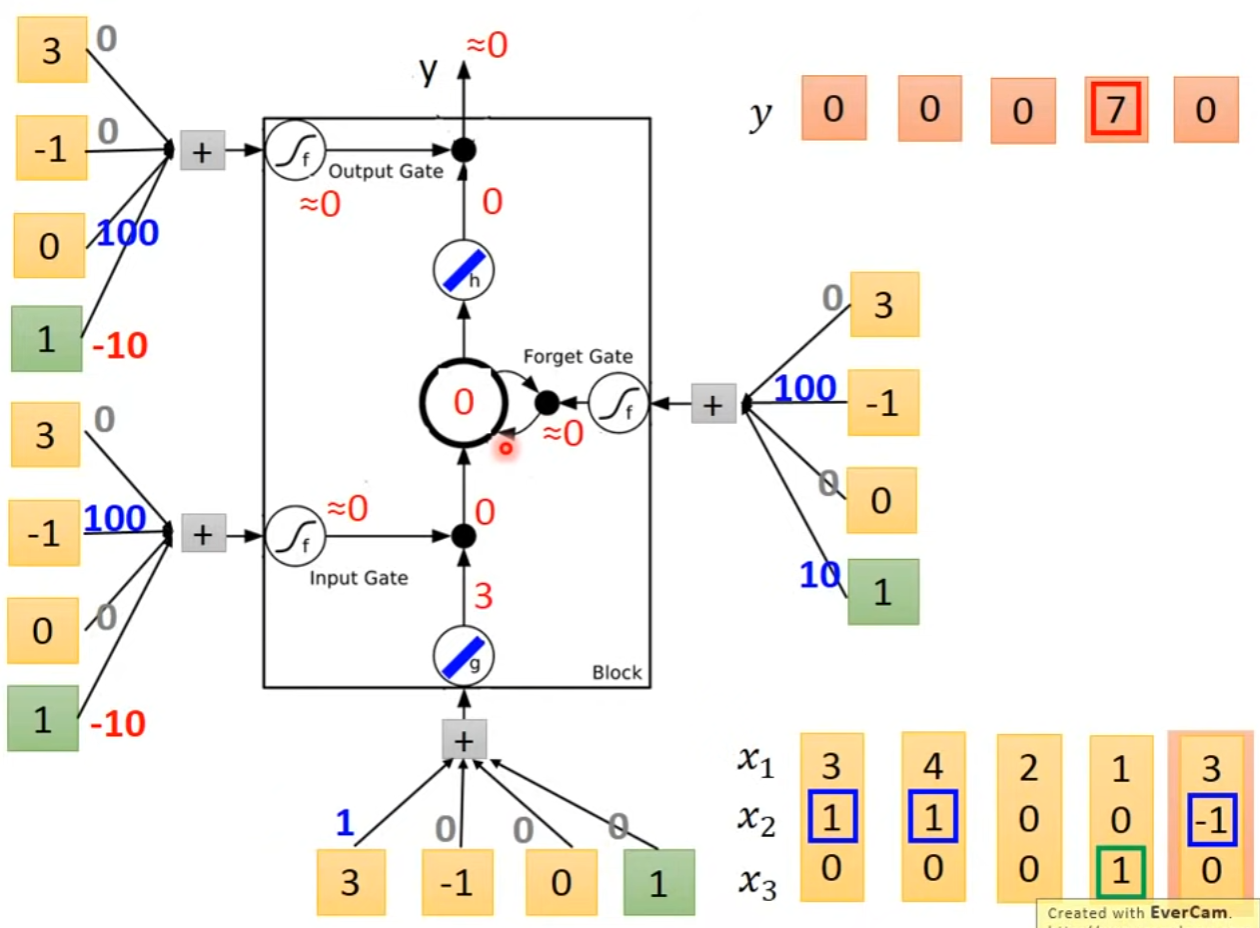
  • 针对记忆单元的输入门、输出门、遗忘门
  • gate常用激活函数为sigmod，表示门打开的程度
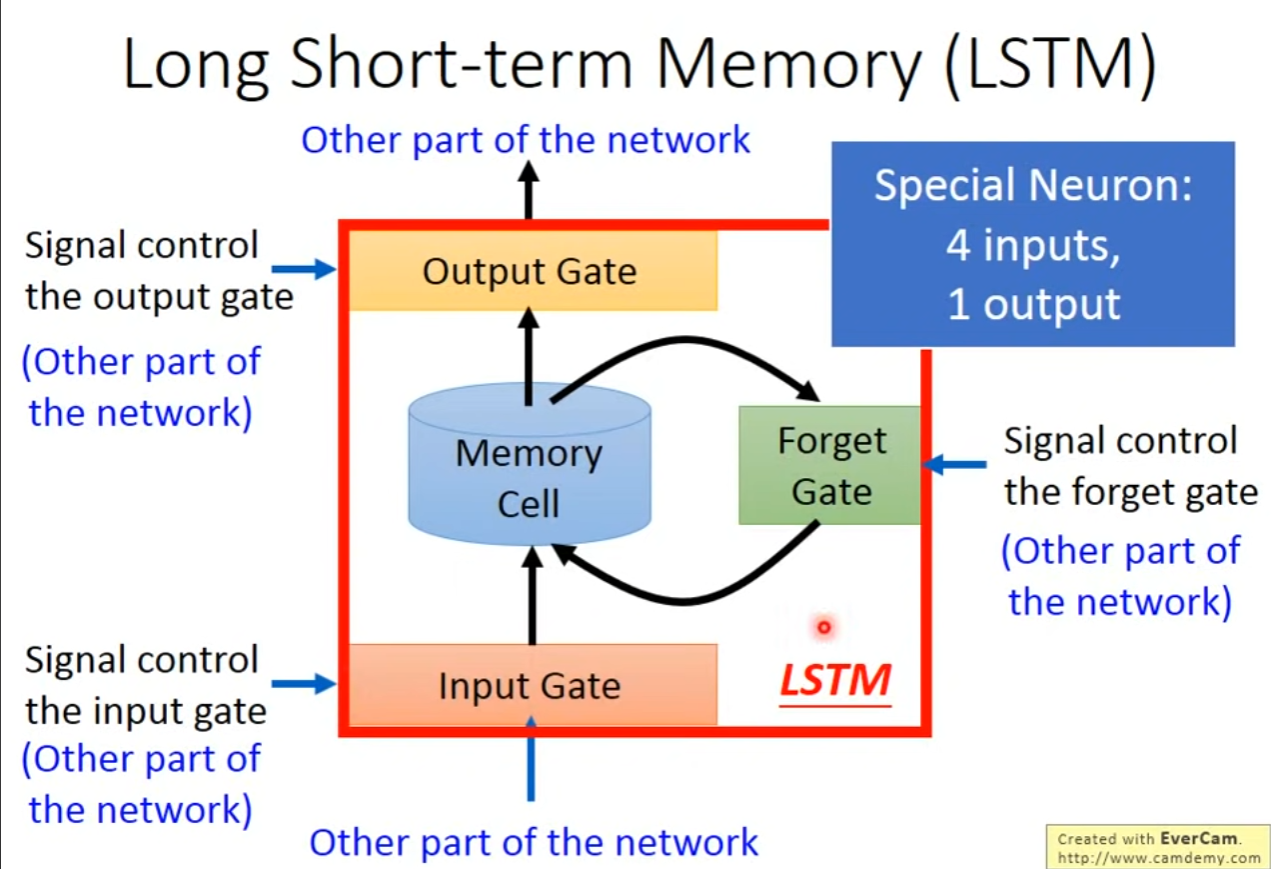
image-20221104172445618
  • 详细结构
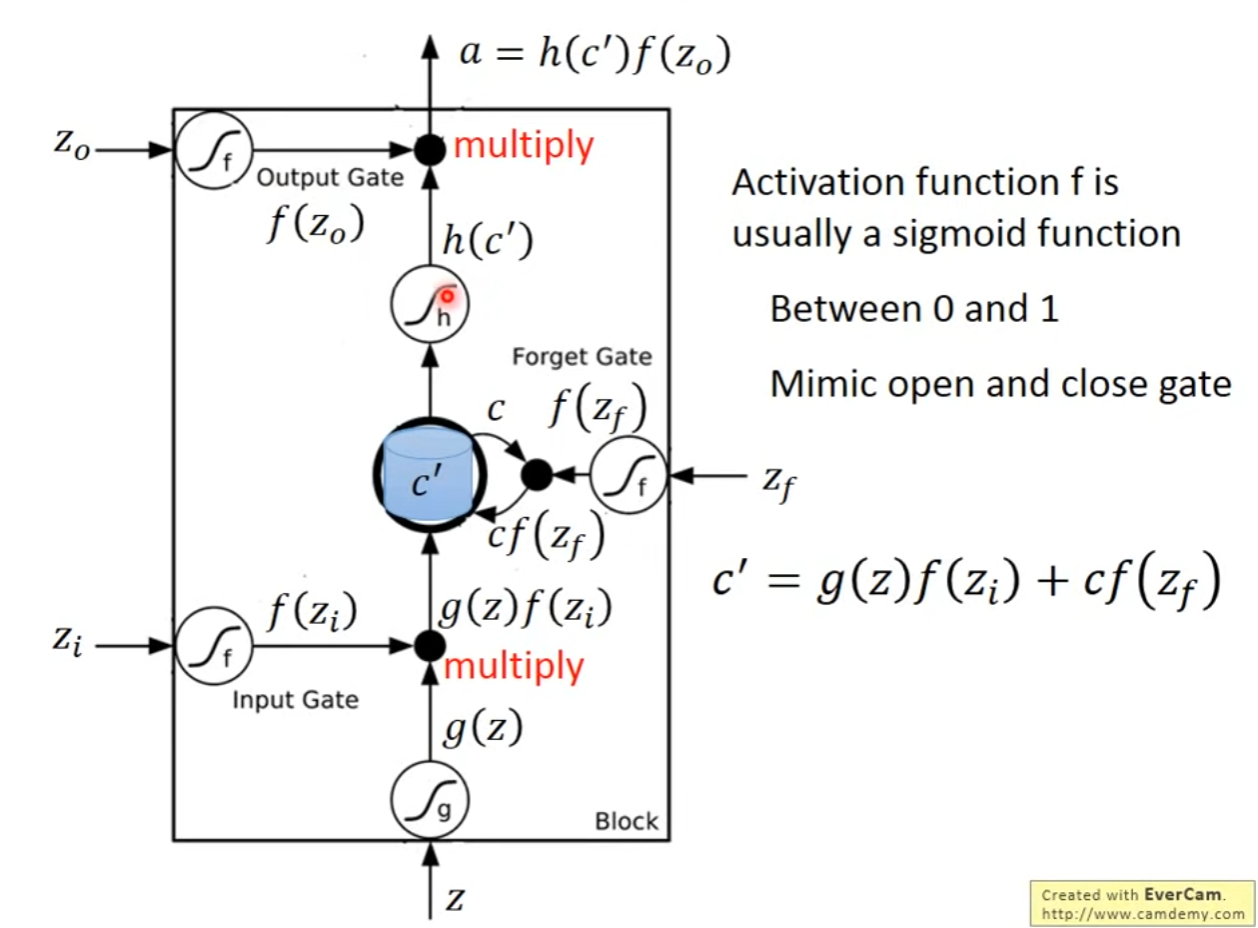
image-20221104173220046
  • LSTM详解
image-20221104195340620
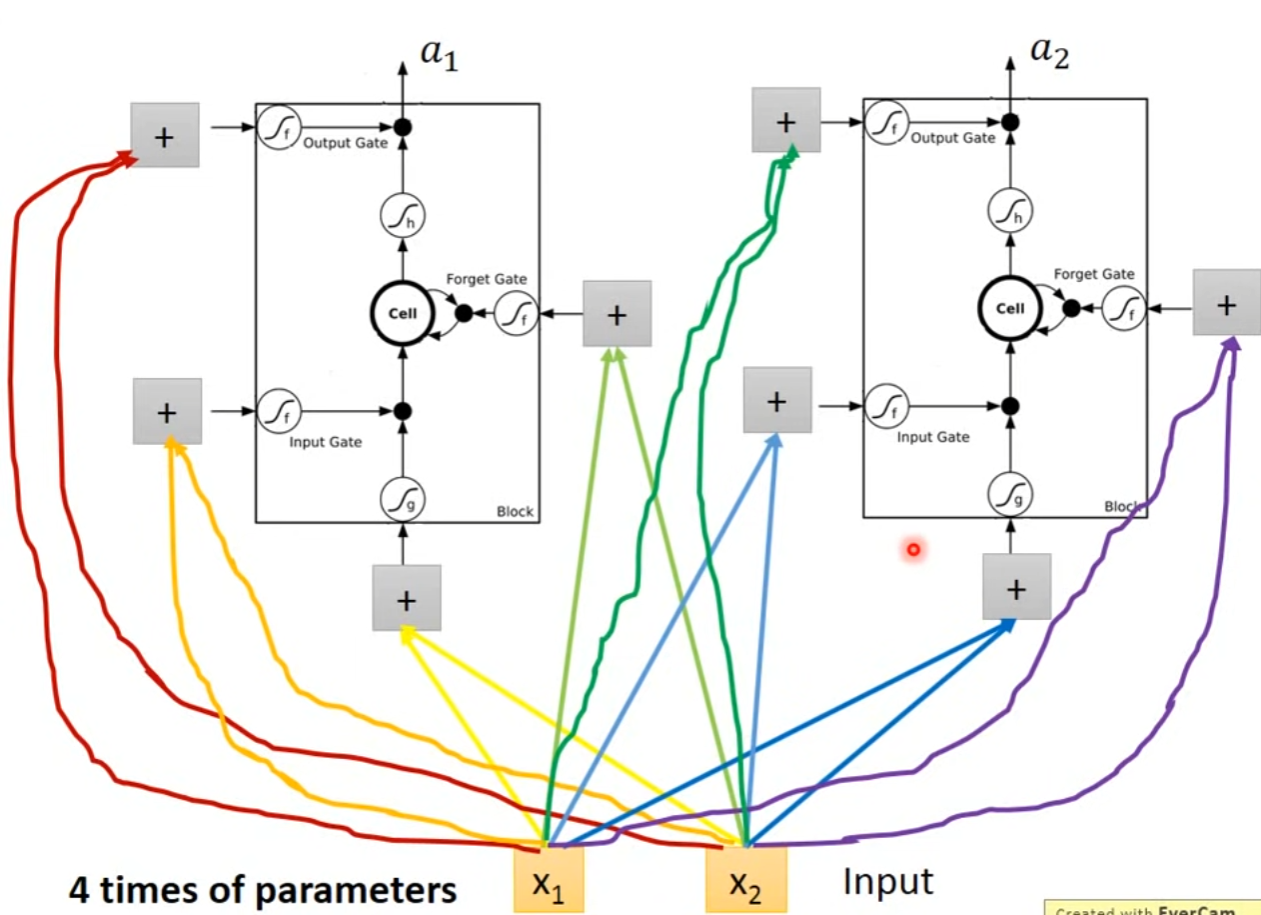
  • LSTM可以替换为原来的RNN的NN节点，分别学习不同的参数，由RNN的一组变为原来的4倍
image-20221104195613746

​

  • 真正的Multiple-layer LSTM，
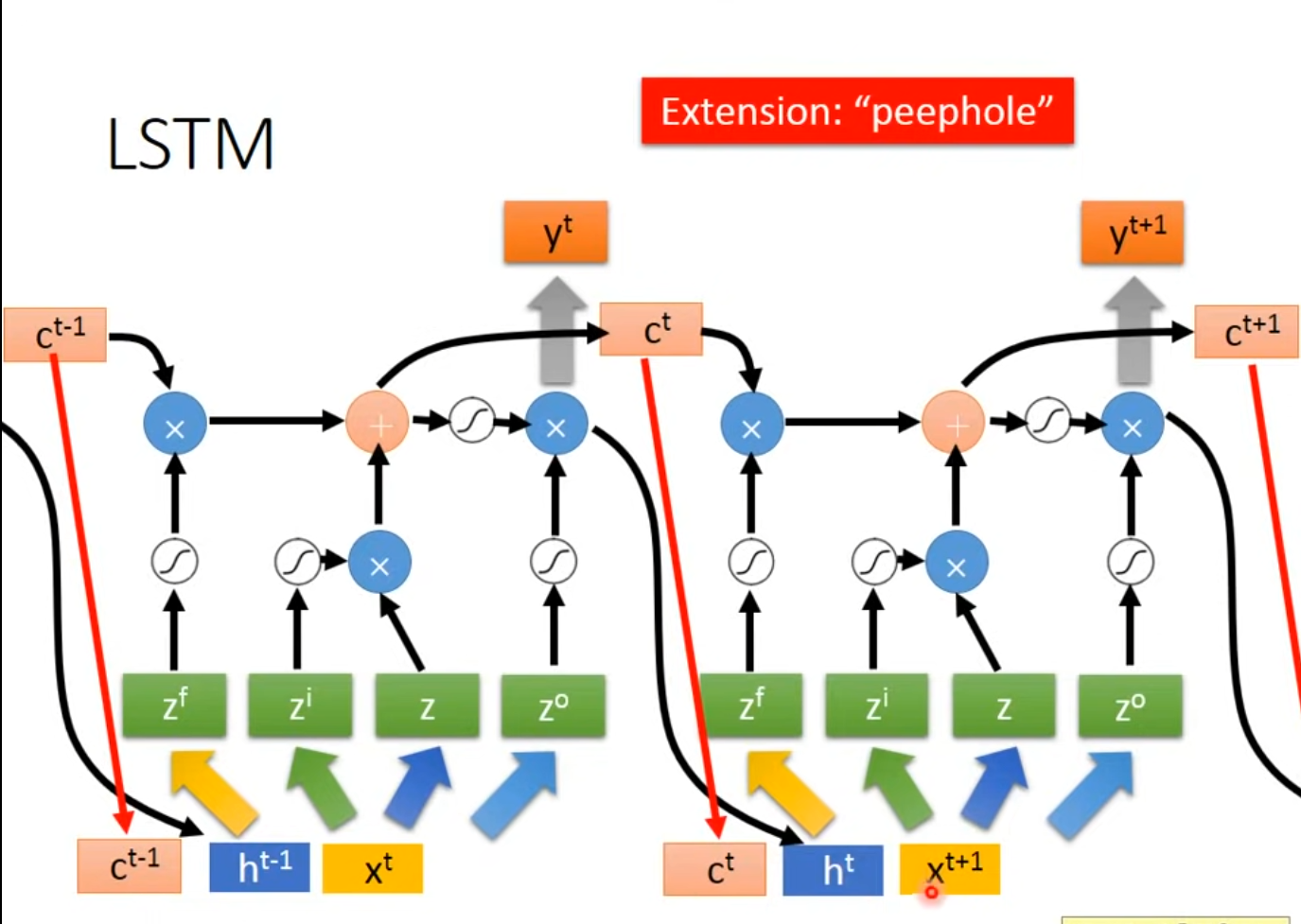
image-20221104200335036

Long Short-Term Memory(LSTM) part2

  • learning target: minimize cross entropy
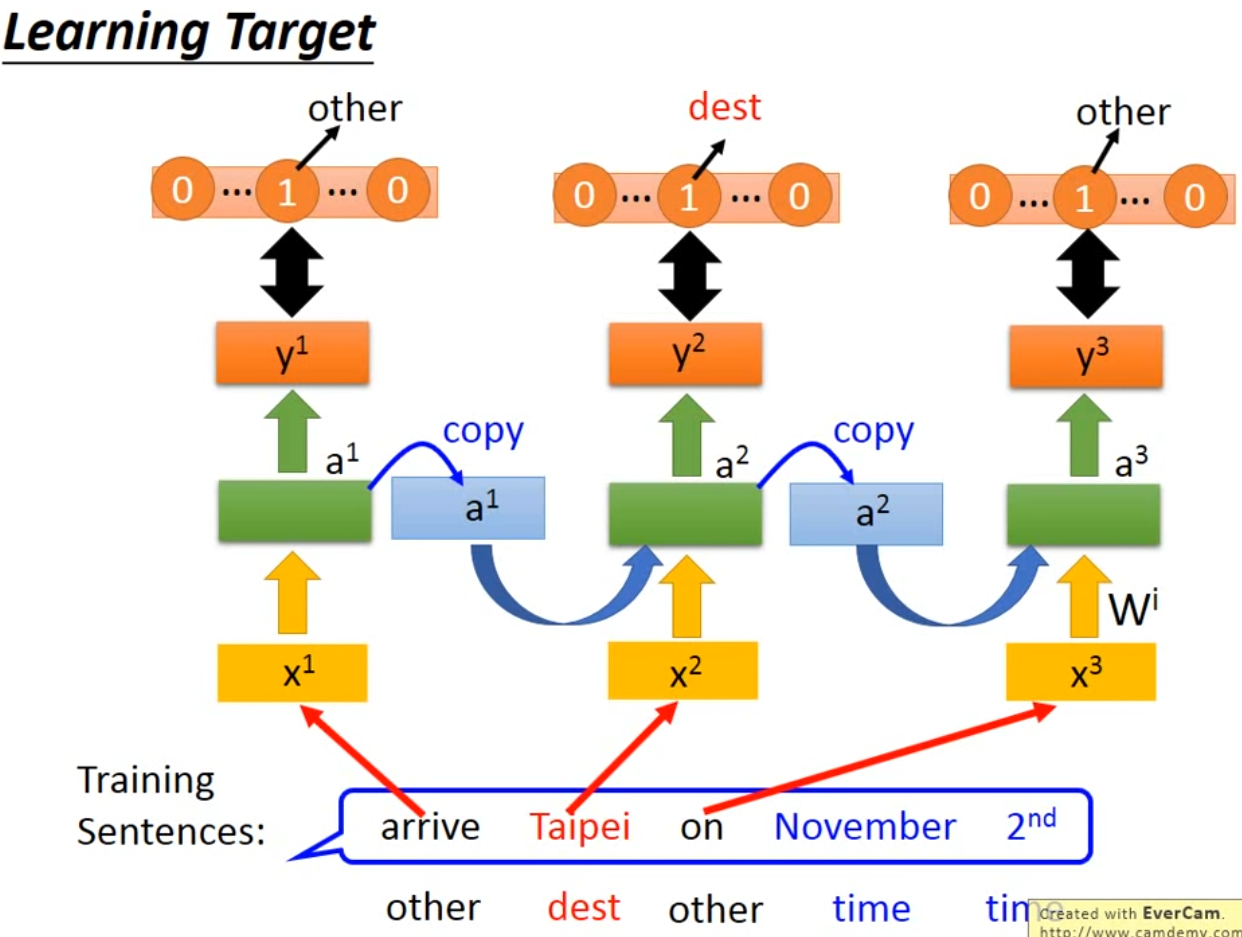
image-20221104201217883
  • learning method: Bachpropagation through time(BPTT)
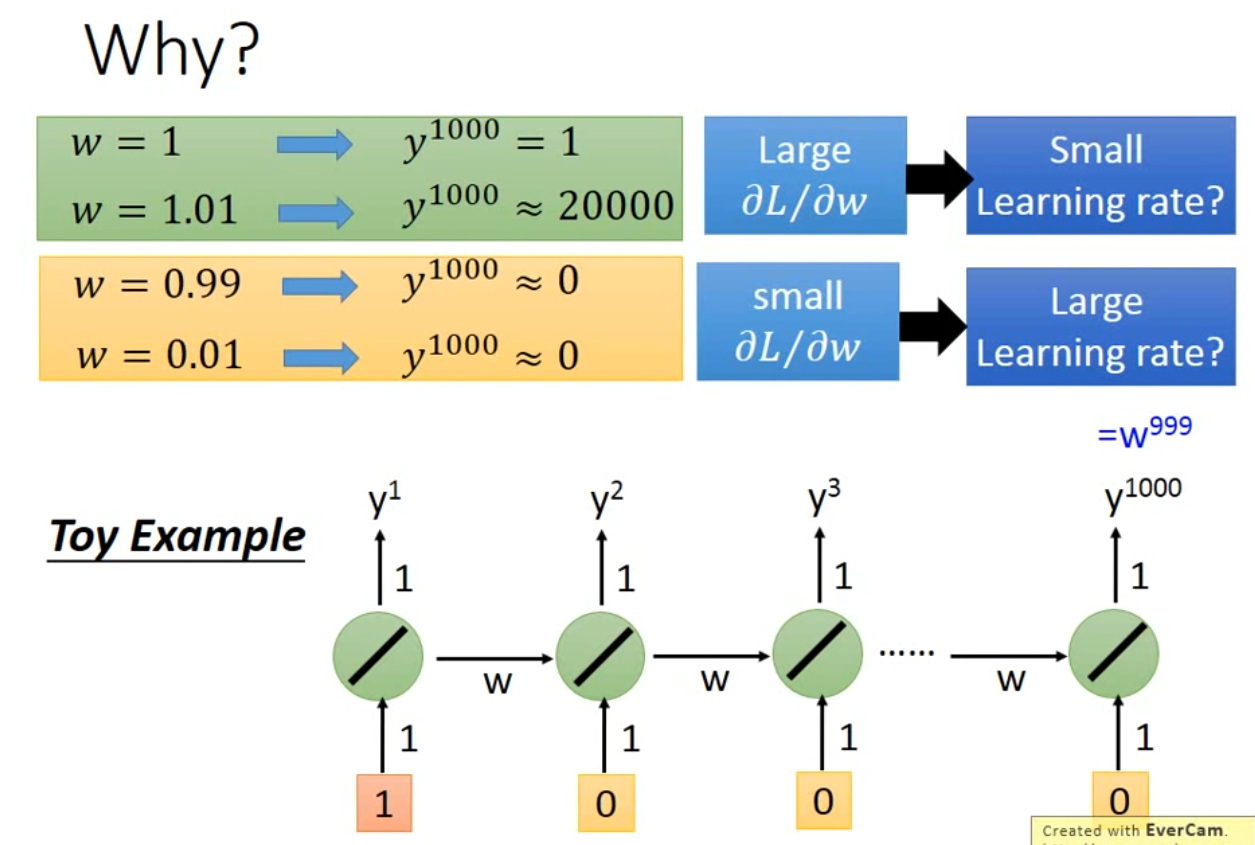
  • 在比较多的地方，RNN对参数比较敏感，可能会导致Loss曲线波动大，可以使用clipping方法，设置gradient阈值比如15，大于15的部分直接设置为15
  • RNN网络结构对w重复利用，造成gradient波动较大
image-20221104202527163 image-20221104203101410 image-20221104203233012

More application：

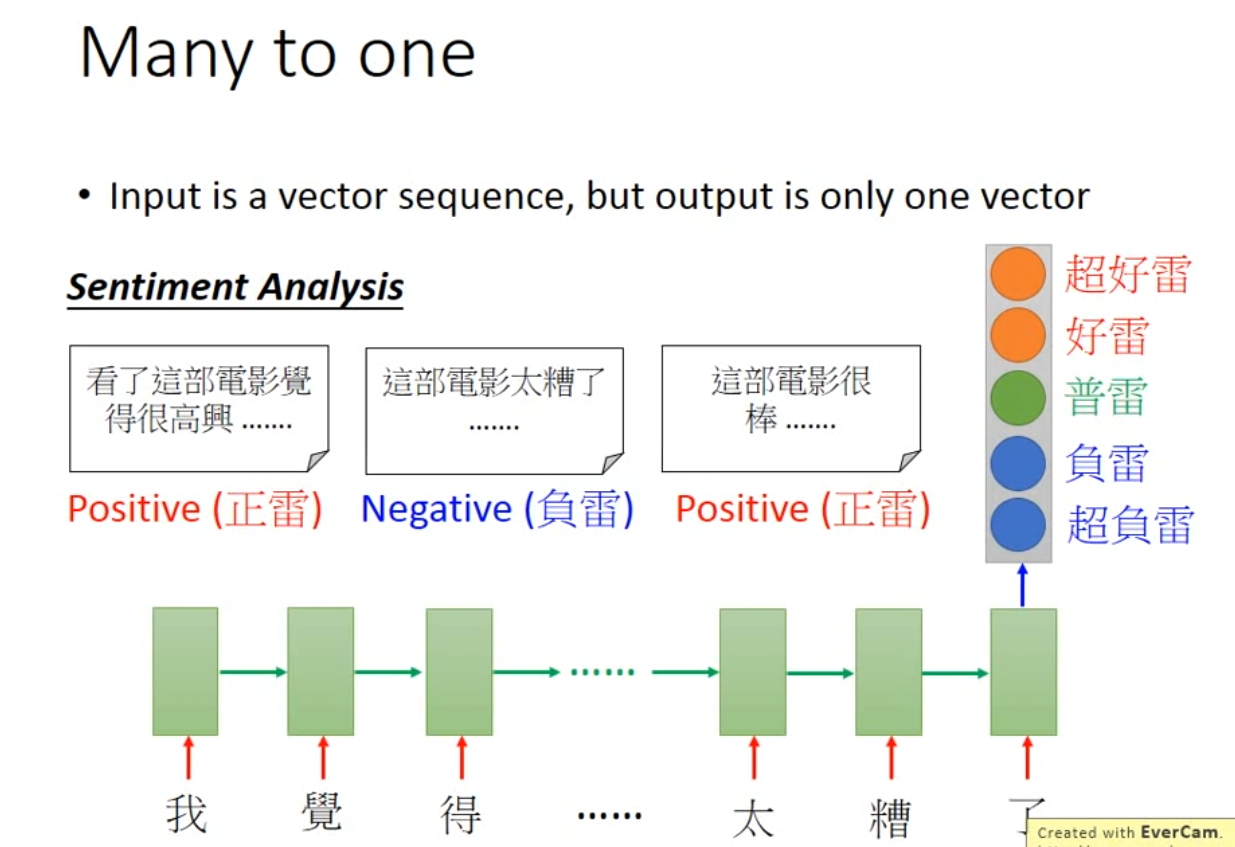
  • Input is a vector sequence, but output is only one vector
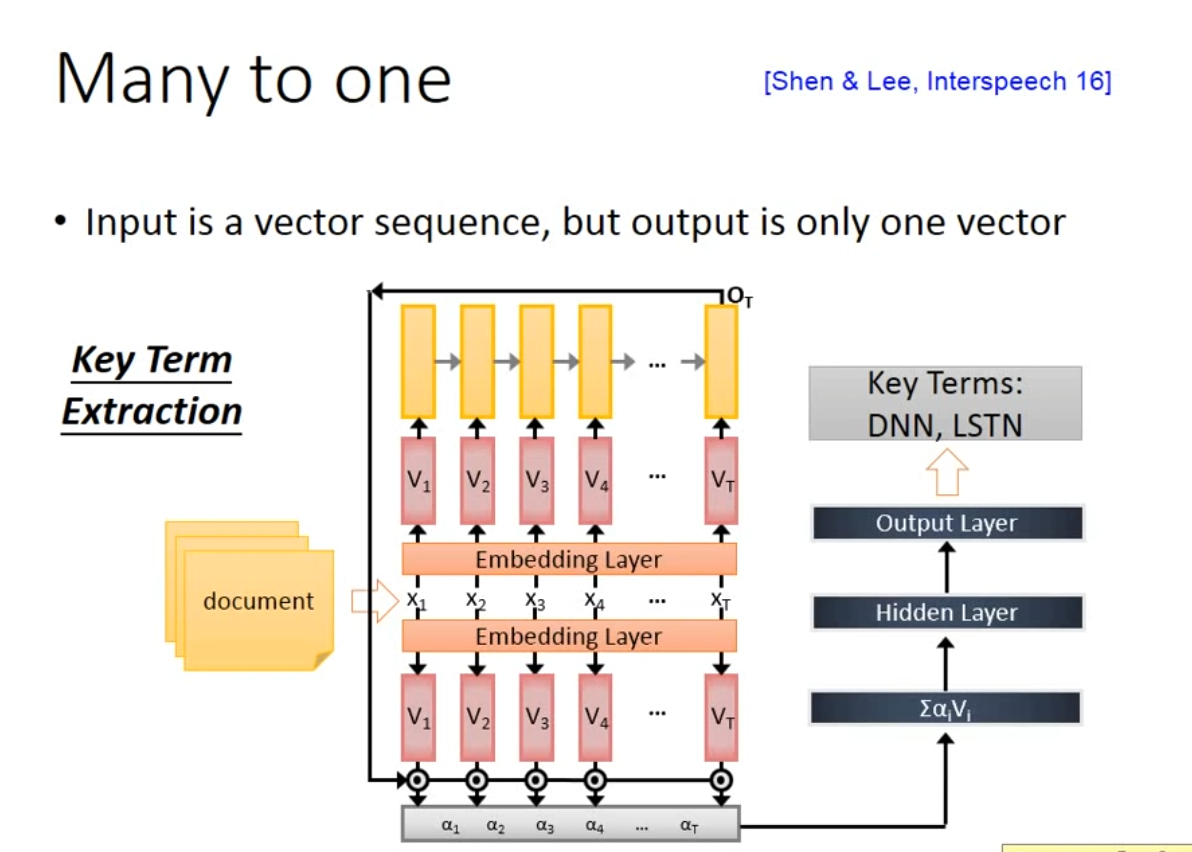
image-20221104203636888 image-20221104203819013

  • Both input and output are both sequences, but the output is shorter.

    • CTC方法，使用null进行补齐，在训练时候穷举所有可能包含null的seq，作为训练集添加
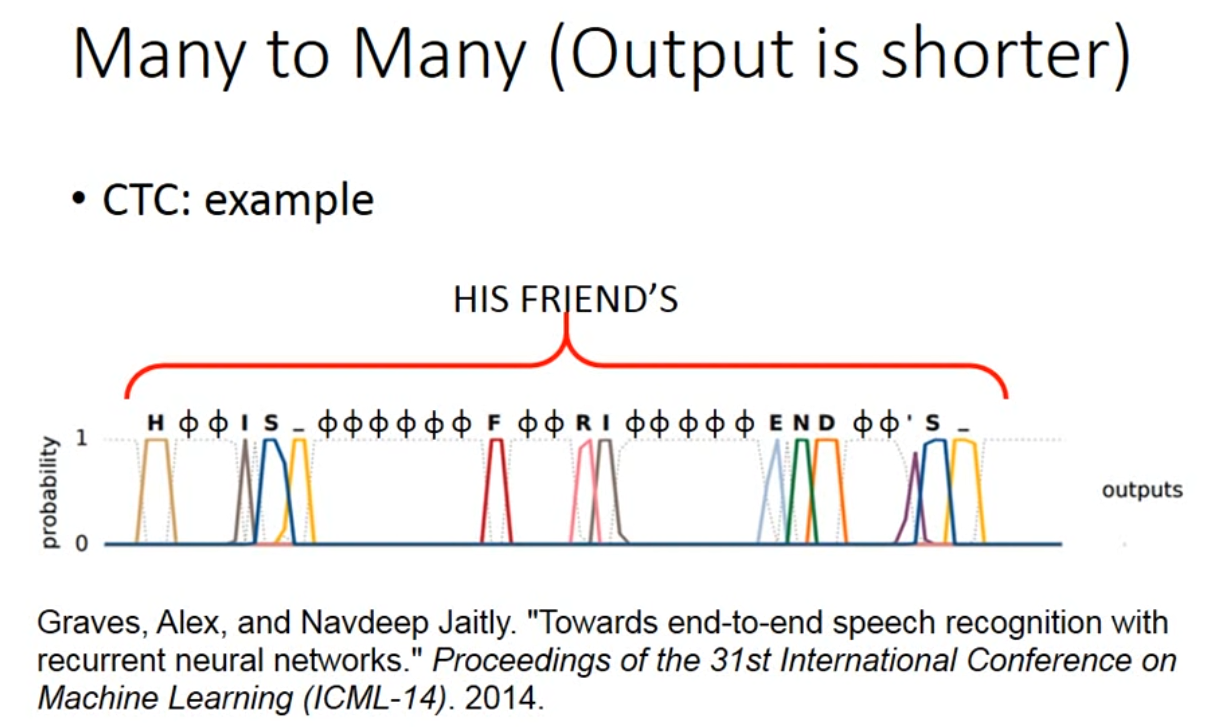
    image-20221104204743570

  • Both input and output are both sequences with different lengths,—>Seq2seq learning

    • 插件机器翻译（需要添加symbol"断"控制输出语句长度）
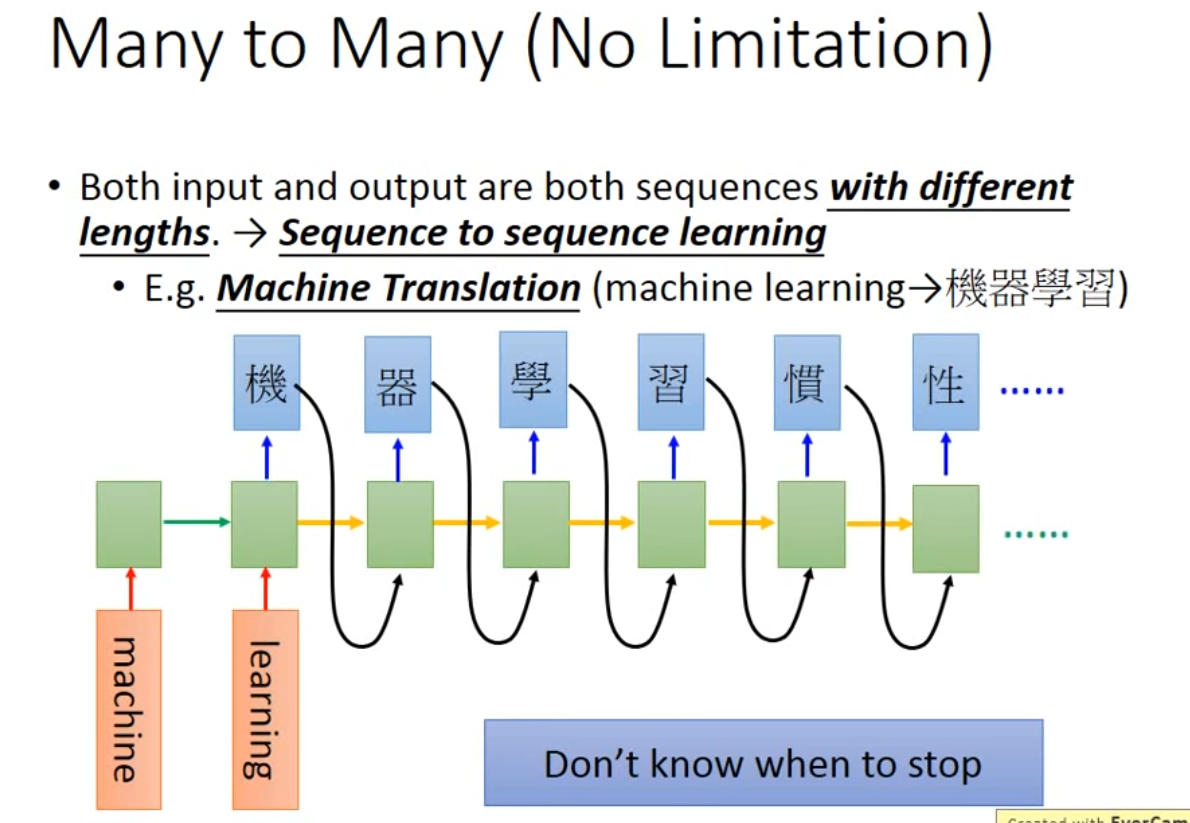
    image-20221104205049900

  • Beyond sequence

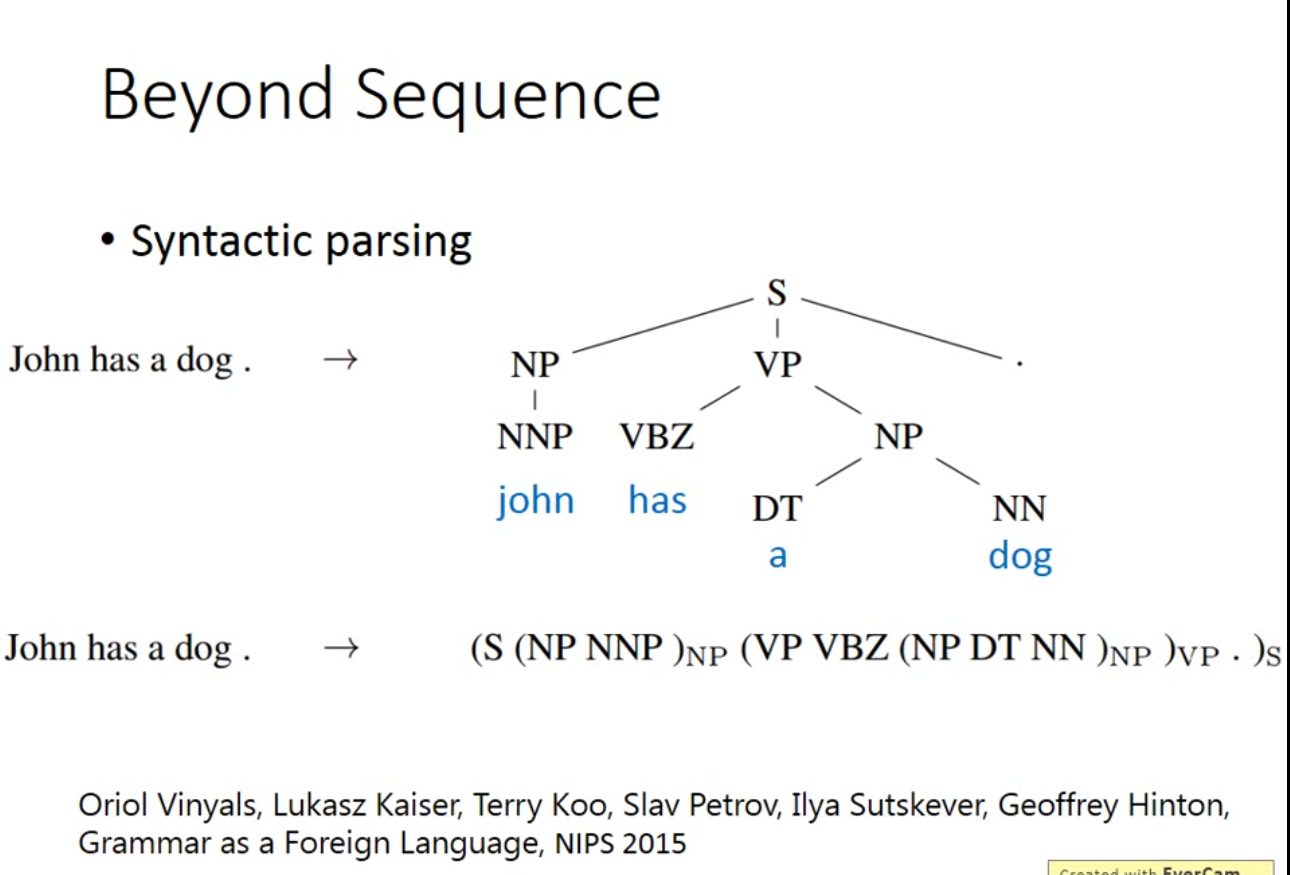
image-20221104205743870 image-20221104212132897
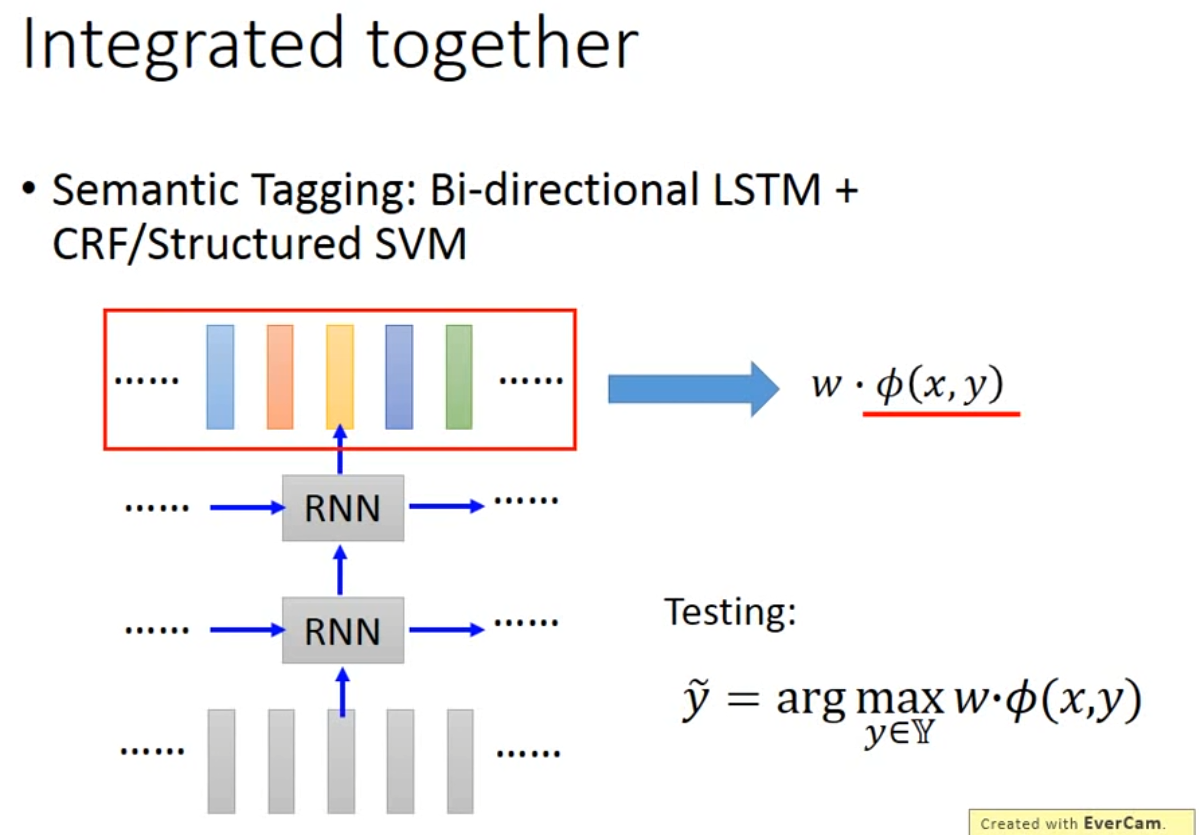
  • Integrated together
image-20221104213200898

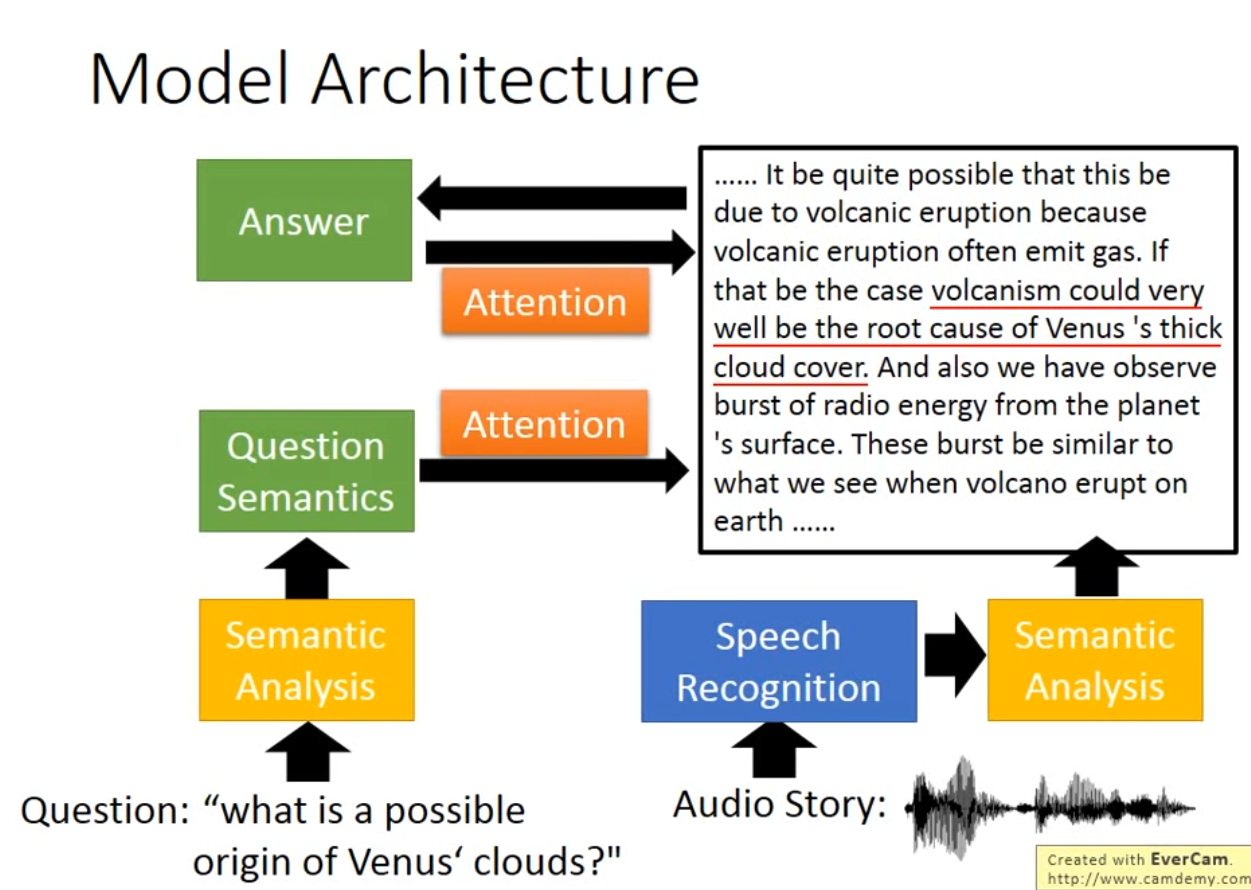
Attention-based model


参考资料:

[1]: 李宏毅：Recurrent Neural Network PartⅠ. https://www.youtube.com/watch?v=xCGidAeyS4M&ab_channel=Hung-yiLee

[2]: 李宏毅：Recurrent Neural Network PartⅡ. https://www.youtube.com/watch?v=rTqmWlnwz_0&ab_channel=Hung-yiLee

[3]: Dive Into Deep Learning. https://d2l.ai/chapter_recurrent-neural-networks/sequence.html

[4]: NLP-文本向量化. https://deeplearning-doc.readthedocs.io/en/latest/deeplearning/NLP/NLP-text-vector.html#